데카르트 좌표계 (Cartesian Coordinate System)
임의의 차원의 유클리드 공간(혹은 좀 더 일반적으로 내적 공간)을 나타내는 좌표계 중 하나입니다. 천장을 날아다니며 옮겨붙는 파리를 통해 영감을 얻어 해당 좌표계를 발명한 프랑스의 철학자이자 수학자인 르네 데카르트의 이름을 따서 지어졌습니다. 2차원 데카르트 좌표계는 좌표평면(coordinate plane), 3차원 데카르트 좌표계는 좌표공간(coordinate space)이라고도 합니다. 직교 좌표계(orthogonal coordinate system)는 데카르트 좌표계를 포함하여 극좌표계, 원통좌표계, 구면좌표계 등 좌표축과 평행한 단위벡터끼리 항상 서로 수직한 모든 좌표계를 총칭하는 표현이다. 데카르트 좌표계는 극좌표계 등 다른 좌표계와 달리, 임의의 차원으로 쉽게 일반화할 수 있습니다. 데카르트 좌표계는 나타내는 대상이 평행 이동에 대한 대칭을 가질 때 유용하나, 회전 대칭 등 다른 꼴의 대칭은 쉽게 나타내지 못한다. 일반적으로 주어진 유클리드 공간에 기저와 원점이 주어지면 이를 이용하여 데카르트 좌표계를 정의할 수 있습니다.
가장 흔하게 볼 수 있는 좌표평면이나 좌표공간의 경우, 데카르트 좌표를 통상적으로 라틴 문자 x, y, z로 적습니다. 4차원인 경우, w나 (물리학에서 시공을 다루는 경우) t를 사용합니다. 임의의 차원의 경우에는 첨자로 xn의 꼴로 사용합니다.
특히 좌표평면은 집합의 정보, 함수의 정보, 다항식의 정보, 행렬의 정보들을 한 공간에서 표현할 수 있는 정보의 통일된 규칙이 적용된다는 점에서 중요한 의미가 있습니다.
또한 이러한 데카르트 좌표계의 정보는 고차원의 데카르트 좌표계뿐만 아니라 다른 좌표계의 정보로 확장될 수 있어 더욱 중요한 의미를 가지며 지금까지도 계속해서 쓰이고 있습니다.
좌표평면
오늘날에 사용하는 좌표평면은 xy평면을 이루는 서로 직교하는 x축(수평 방향)과 y축(수직 방향)으로 정의한다. x축과 y축이 만나는 점을 원점이라고 부릅니다.

좌표평면의 사분면(quadrant)은 x축, y축으로 나뉘는 좌표평면 상의 네 부분을 말한다. 제1사분면 ~ 제4사분면으로 나뉩니다.
제1사분면은(+,+) 제2사분면은(-,+) 제3사분면은(-,-) 제4사분면은(+,-)
좌표공간
오늘날에 사용하는 좌표공간은 xy평면, xz평면, yz평면으로 이루어지는데 이 세 평면은 서로 직교하며 평면을 이루는 x축(수평 방향)과 y축(수직 방향) 그리고 z축 또한 서로 직교한다. x, y, z축이 만나는 점을 원점이라고 부릅니다.
극좌표계 (Polar Coordinate System)
평면 위의 위치를 각도와 거리를 써서 나타내는 2차원 좌표계입니다. 극좌표계는 두 점 사이의 관계가 각이나 거리로 쉽게 표현되는 경우에 가장 유용합니다. 직교 좌표계에서는 삼각함수로 복잡하게 나타나는 관계가 극좌표계에서는 간단하게 표현되는 경우가 많습니다. 2차원 좌표계이기 때문에 극좌표는 반지름 성분과 각 성분의 두 성분으로 결정되며 주로 r 로 나타내는 반지름 성분은 극(데카르트 좌표에서 원점)에서의 거리를 나타냅니다. 주로 θ 로 나타내는 각 성분은 0°(직교 좌표계에서 x축의 양의 방향에 해당)에서 반시계 방향으로 잰 각의 크기를 나타냅니다.

극좌표를 이용한 점의 표시
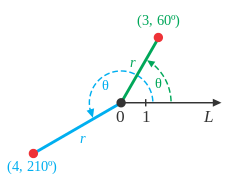
극좌표계의 점은 반지름(r)과 각(θ)로 표현됩니다. r은 극에서의 거리를 의미하고, θ는 0°(직교 좌표계의 x축 양의 방향에 해당)에서의 각도를 의미합니다. 만약 r이 음의 값을 갖는다면, θ가 가리키는 방향과 반대방향으로 거리 |r|만큼 떨어진 점을 뜻합니다.
예를 들어, 극좌표 (3, 60°)는 극에서 60° 방향으로 3단위만큼 떨어진 곳을 나타냅니다. 극좌표 (3, -300°)도 같은 위치에 그려집니다.
데카르트 좌표와는 달리 극좌표에서는 하나의 점을 나타내는 방법이 무한히 많습니다. 여러 바퀴를 돌아 제자리에 돌아와도 위치는 변하지 않기 때문입니다. 일반적으로 (r, θ)는
(r, θ ± n×360°) 또는 (−r, θ ± (2n+1)×180°)
로 표현될 수 있습니다(n은 임의의 정수).
(0, θ)는 일반적으로 극을 뜻하며, 반지름이 0이기 때문에 어떠한 각이든 상관이 없습니다. 점을 나타내는 방법을 하나로 제한할 때에는 r은 양수로, θ는 구간 [0, 360°) 또는 (−180°, 180°](라디안으로는 [0, 2π) 또는 (−π, π])의 수로 하는 것이 보통입니다.
극좌표의 각은 라디안을 이용한 호도법으로도 표현할 수 있으며(2π rad = 360°), 이는 상황에 따라 다릅니다. 항행에서는 60분법으로 각을 나타내며, 물리 분야(특히 회전 역학)와 거의 모든 미적분에서는 호도법이 쓰입니다.
극좌표와 데카르트 좌표 사이의 변환

그림. 극좌표와 데카르트 좌표 사이의 관계를 묘사
r 와 θ 는 삼각함수를 이용해 데카르트 좌표의 x와 y로 변환할 수 있습니다.
x = r cos θ
y = r sin θ
데카르트 좌표의 x 와 y 는 극좌표의 r 로 변환할 수 있습니다.
r 2 = x 2 + y 2
(피타고라스 정리 사용)
θ를 정의할 때는 다음과 같은 사항을 고려해야 합니다.
- r = 0 일 때는 θ는 임의의 실수가 될 수 있습니다.
- r ≠ 0 일 때는 표현의 유일성을 위하여 크기가 2π보다 작은 구간으로 한정합니다. 보통은 [0, 2π) 나 (−π, π]가 사용됩니다.
[0, 2π)에 한정할 때는 다음과 같은 함수를 사용합니다. (arctan 는 tan 의 역함수입니다.)
(−π, π]에 한정할 때는 다음과 같은 함수가 사용합니다.
원통 좌표계 (Cylindrical Coordinate System)
극좌표계는 원통좌표계와 구면좌표계로 확장할 수 있으며, 이 두 가지는 2차원의 극좌표계를 포함한다. 원통좌표계는 거리 좌표를 더해 극좌표계를 확장시키며, 구면좌표계는 각 좌표를 더해 확장합니다.
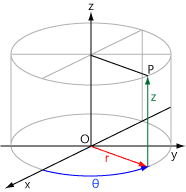
원통 좌표계는 평면 극좌표로 (0,0)을 제외한 xy 평면 전체를 일대일 대응시킬 수 있으므로, 여기에 z축을 더하여, 3차원 공간을 표현할 수 있습니다. 평면 극좌표계의 r, θ, 그리고 z로 이루어지는 이 좌표계를 원통 좌표계라고 합니다. 원통 좌표계란 이름이 붙은 이유는, 세 좌표 중 r이 고정되고, θ, z가 임의의 값을 취할 수 있을 때의 자취가 원통이기 때문입니다. 원통 좌표계의 특이점은 z축 위의 점들입니다.
세 가지 원통 좌표계의 좌표들은 다음과 같은 공식을 써서 데카르트 좌표로 변환할 수 있습니다.
구면 좌표계 (Spherical Coordinate System)
구면좌표계는 원점에서의 거리 r, z축 양의 방향과 이루는 각 'θ', xy 평면으로의 사영이 x축 양의 방향과 이루는 각 φ, 이 세 가지 변수 r,θ,φ로 이루어지는 좌표계입니다.
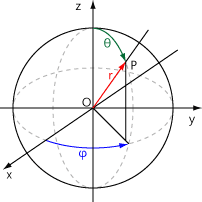
특이점은 r=0 이거나, θ=nπ(단, n은 자연수)를 만족하는 모든 (r,θ,φ)이며, 직교 좌표계에선 각각 (x,y,z)=(0,0,0), z축에 해당합니다. 구면 좌표계는 r을 고정시켰을 때의 자취가 원점을 중심으로 하는 구이기 때문에 붙여진 이름입니다.
구면좌표계의 r은 원점과의 거리인 반면 원통 좌표계의 r은 z축과의 거리입니다. 따라서 이를 구분하기 위해 원통 좌표계의 반지름을 r대신 ρ를 써서 표기하기도 합니다. 원통 좌표계의 θ는 구면좌표계의 θ가 아닌, φ와 일치합니다. 또한 이 좌표계는 지구의 지도에 사용되는 위도, 경도와 비슷합니다. 위도 δ는 'θ'의 여각이며(δ = 90° − 'θ'), 경도 ℓ 은 ℓ = 'φ' − 180°와 같이 정의합니다.
세 가지 구면좌표계의 좌표들은 다음과 같은 공식으로 직교 좌표로 변환할 수 있습니다.
참고사이트
'GIS > GIS Terminology' 카테고리의 다른 글
| WKT(Well-Known Text) (0) | 2023.04.12 |
|---|---|
| 지구타원체, 편평률(flatterning)과 이심률(eccentricity) (0) | 2023.04.10 |
| GeoJSON 데이터 형식 알아보기 (0) | 2023.02.07 |
| GPX, KML, GeoJSON (0) | 2022.10.04 |
| 래스터(Raster)와 벡터(Vector) 차이 (0) | 2022.06.14 |








